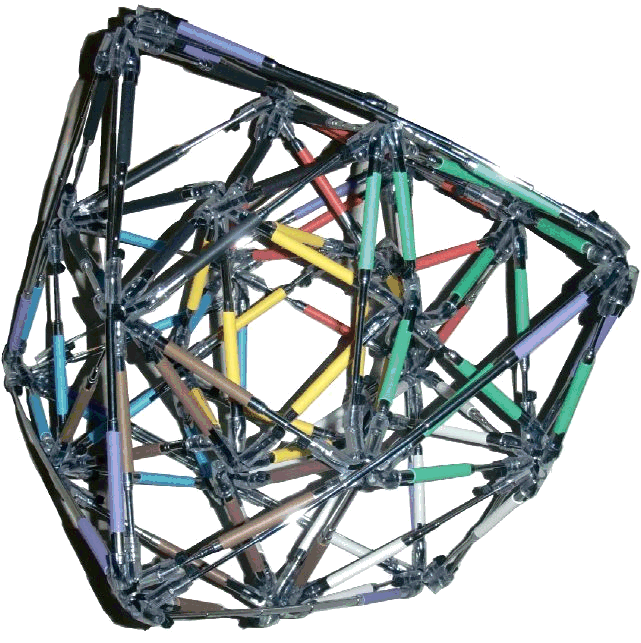
Figure 1: The Colossus Puzzle (made of 96 telescopic rods), based on
the four dimensional super symmetry of the Icositetrachoron (24-cell).

"Imagine a cave, where prisoners who have been chained up since childhood sit facing a wall unable to turn their heads. They can only see shadows that are cast on the wall by a light from behind them. As they are unable to turn around and see what is behind them, they come to believe that the world of shadows is real. We probably do the same in the way that we perceive our own world."

Plato, 428-348 BC

Graph Theory and Symmetry

The first thing that a normal cuber thinks when he hears of a "higher dimensional puzzle" is the 4D representation of the Rubik's Cube. It is surely a great challenge, but here, we are not interested in virtual puzzle solving. Instead, we will start from the basics, using the symmetry of the simplest higher dimensional structures such as the smallest polytopes.

Algebraic Graph Theory focuses on the symmetric properties of graphs made of vertices and edges. Depending on the labeling of those vertices and edges, and the way they were connected (including overlapping), we are able to differentiate the dimensionality.

Vertex and/or edge transitivity (a property of whether one vertex or edge can be swapped by another and keeping the structure and its properties invariant) is very important to applying this symmetry. And by achieving this, we can use some exceptional symmetry that belongs to structures which are not only two or three-dimensional, but four dimensional and beyond.

The Fourth Dimension

So how can someone claim that we can create puzzles which are four (or higher) dimensional? Well, no one can claim that a puzzle is four dimensional in our 3D world. But we may certainly use the symmetry that comes from such structures.

The fourth dimension can be claimed to be related to either time or space (and there is a debate about it). Here is my personal attempt to unify the time and space notions. 4D shapes exist in four spatial dimensions, where the fourth dimension is not time, but a dimension of space. As we live in three spatial dimensions, we cannot see in four spatial dimensions. Now, 4D shapes consist of 3D slices, just like a 3D cube can be thought of as having 2D square slices. So viewing a sequence of these 3D slices is equivalent to a 4D being seeing the depth of the four spatial dimensions. Therefore, by watching the 3D projections in a sequence, it is possible to substitute the fourth spatial dimension by time, which is assumed to be zero.

But can we assume that time is zero? As agreed by top mathematicians and physicists, time can certainly be assumed to be constant for a while, because as stated here, "time is a tiny window of a much greater underlying fabric, which ultimately encompasses the multiverse of all possible universes and quantum indeterminacy". And this explains why we are allowed to use this way to experience the symmetry of the four dimensions.

The Legend of the Pyramid, a very entertaining mini-story is highly recommended and it provides a more "comparable" approach from our 3D world point of view.

The Construction of the Graphidrons

Typical one-piece mechanical puzzles have rotating and/or sliding parts. In recent years, many new mechanisms allowing new types of movement have been presented. The Hoberman Brain-Twist which uses the duality property is one of the most striking structures to date. This design always keeps invariant the original positions of its vertices and only changes the color of the petals which are built on those vertices.

But what if we had a structure whose edges and vertices had a sophisticated symmetry allowing them to interchange places? We now define the Inside-Out-Turn (IOT) as:

"The sequence of moving one or more corners/vertices (connected or not) of a one-piece mathematical puzzle (which has deforming, expandable or flexible edges), through a hole defined by three or more vertices/corners of the same puzzle."

Figure 2: When we perform the IOT on a Hypercube, an entire square (defined by four vertices) moves through the opposite square side.

One of the biggest hurdles is to be able to make those designs flexible enough so that they can carry such higher dimensional symmetries. A good start would be constructing simple (as possible) structures based on 4D symmetry. But in the four dimensions, length is not perceived the same way as in the three dimensions. In fact, theoretically speaking, the length of any part of a 4D object which is "visiting" our 3D space can range from zero to infinite!

Therefore, the edges (connecting the vertices) should be able to adjust their lengths, or in other words to expand and contract. This is achievable by using telescopic rods or by using another type of flexible, foldable, or expandable material.

The way to connect the rods is also of critical importance. A powerful symmetry can allow two vertices to interchange positions while keeping the positions of the rest (or most of the rest) of the vertices invariant. But that immediately poses a question: How to ensure that there is no overlapping of the tips of the rods which could cause unwanted breakages?

More than one solution to this problem is available, and is related to efficiently and strategically placing the rods within "substructures" and then reconnecting them. That could be a subdivision to 3D solids, 2D polygons, or (in cases where the valency - the number of rods connected to one vertex - is an odd number) single rods. The main aim is to ensure that when staring at one state we should always be allowed to reach any next existing state without causing extra pressure to the joints.

The Pentachoron (also known as 5-Cell, 4-Simplex, Hyper-Pyramid, or Complete Graph K5), is the smallest possible structure of higher than three dimensions. Just like a tetrahedron in the third dimension, its structure allow the exchange of an edge with any other of its edges (edge-transitive) and any vertex with any other of its vertices (vertex-transitive). In a real world structure, dividing the Pentachoron into two triangles and a square, and having them connected with five swivel connectors, is vital in providing the required flexibility for it to function in a robust way.

The Hypercube (also known as 8-Cell or Tesseract), due to its orthogonality and bipartite graph properties, can be constructed in many ways. For example, one may only join simple rods with a little but of flexibility at the ends, but it can also be easily divided into eight squares, or even four octagons.

All those structures, of any dimension (1D, 2D, 3D, 4D, 5D, 6D, etc) will be referred to as Graphidrons.

The entire theory of a polytope of a higher dimension relies on the fact that at all times all vertices are equidistant from each other. In our three dimensions, it is not possible to have a 4D or 5D polytope with all edges equal (because the notion of the distance is perceived differently). But by manipulating a 3D structure whose distances between the corners change, they may all reach similar lengths at a different time.
Assuming that the time of this manipulation is constant, allows us to simulate the properties of a 4D object. But which object should be used as a reference? In general, 3D objects which are projections of four or more dimensional objects, always have internal and external edges. Based on the external edges (because they are the ones defining the shape), there are several options for shapes. For example:
1. The minimum external edges shape (MINEES), where all external edges should be of minimum length.
2. The maximum external edges shape (MAXEES), where all external edges should be of maximum length.
3. If none of the above two applies, we may still give to the projection the shape of a known solid (KSEES) with a combination of extended and contracted external edges.
Note that, a given 4D symmetry puzzle may have all the variations described above, always depending on theme colors given to the edges and/or vertices.

A Current List of Graphidrons

1. Chronos (Plato's First Shadow)

Chronos (named by the ancient God of Time) is more than just a puzzle. It is the first non-virtual four-dimensional symmetry object ever presented to this world. While solving it, we are forced to view all 3D projections of the 4D polytope Pentachoron. And by assuming that time (the fourth dimension!) is constant during the manipulation of the puzzle, means that we "instantly view" all 3D projections. Therefore, we have the equivalent of a four-dimensional object in our very hands.

Figure 3: The Chronos and Galaxius puzzles based on the Pentachoron.

The symmetric properties of the Chronos puzzle are stretching the boundaries of imagination. Its self-dual property ensures that any vertex can exchange with any other vertex while keeping the rest of the puzzle invariant. This fact, combined with a deceitfully simple, yet mathematically complex mechanism, provides a mesmerizing trip to other dimensions, never experienced before by three dimensional living beings.

By using the MINEES shape and minimizing the nine external edges (which forces the internal edge to become extended), we always get the shape of the triangular dipyramid. And as amazing as it sounds, any of the ten edges can be shifted (by using IOTs) to the middle of the triangular dipyramid. It is a testament to the four dimensional symmetry that this puzzle has.

The goal of the puzzle is to ensure the internal edge changes to all ten different colors by using the same IOT (which can be applied from six different starting points). During this process, we should not go through the same color twice. It may sound easy, but a good strategy is required. This is because there are three types of edges. The internal edge (Type I), the edges which are directly related to the internal edge (Type II), and those indirectly related to the internal edge (Type III). The six ones at the top and bottom are Type II, and the three in the central row are Type III. And we cannot go from Type I to Type III edges without passing through the Type II edges. Thus, there exist some unexpected "road blocks" and the solver has to be careful.

More puzzles (requiring different solutions) may be defined based on the very same structure, by just using different colors or a different 3D projection as a basis.

2. Ananke

This puzzle is similar to Chronos, but this time, it is the vertices which are colored, not the edges. The goal here is to prove that any positioning of one vertex with respect to the rest is possible.

3. Galaxius (and the 5-cell cage).

Here, all edges are of the same color except for a black one (which starts as Type I) and a golden one (which starts as Type III). The goal is to turn the golden edge into Type I. This puzzle has been used as the exchange puzzle for the International Puzzle Party 31 in Berlin.

The goal here is to free the golden civilization (golden rod) and then trap the black hole (black rod) by turning it into an internal edge. The rest of the same colored rods represent the Universe. But you should never underestimate the black hole's universal dominance, as its vast gravitational power may affect your mind forcing you to re-capture the golden civilization! So this puzzle is essentially representing a never ending battle between good and evil in a higher dimension.

3. Houlis Cube

Figure 4: The Houlis Cube, based on the 16-cell, is the only known structure
whose different states can take the shape of a cube, a tetrahedron, and more!

The Houlis Cube is a personal favourite for many reasons. It is based on the symmetry of the 4D polytope known as hexadecachoron (or 16-cell). It is called "Houlis Cube" because of the X crosses which exist on each side of the cube (the Greek letter "Xi" is the first letter of my name, and it is pronounced as "H" in English).

The cubic state of this puzzle is a KSEES shape, and in its solved state all crosses are made of two edges of the same color. There are sixteen different cubic states only and going from one to another requires the movement of no less than three vertices. Two of those cubic states are solved states and are mirror images of each other. The goal is to go from one mirror image to the other. There are many more interesting (cubic or not) patterns than can be made with this puzzle, which is very stable by design.

5. Pegasus and Infinity.

Unlike Chronos, Pegasus uses an even higher symmetry, which this time is derived from the fifth dimensional 5-Simplex (equivalent to the complete graph K6). This equips the puzzle with more complex symmetry, parts, and consequently, IOT moves. More specifically, when using the MINEES shape (which provides to the puzzle a unique "Pegasus" horse-like shape), we have now three different choices for IOTs, compared to only one found in Chronos.

By using those three moves (and studying their outcomes), as much amazing as it sounds, we may create any color combination between the vertices.

An interesting attribute is the choice of having different (mechanically) designs, depending on the how specific edges overlap others. For example, the 5-Simplex (and going further the 6-Simplex etc) which is derived from the corresponding 5D symmetry design, was found to have both manipulable and non-manipulable state configurations. This is because, with an increasing amount of edges, the spacial (knot) placement of those edges, matters for making the structure a "good puzzle challenge" or a "too stabilised puzzle piece of art which is good only for decorative purposes".

For the Chronos puzzle, changing the crossing will not matter much, as its simple design will only switch between two "universes" (and of course, this fact does not prevent it from taking the shape of all 3D projections). However, when we deal with structures of higher dimensional symmetry (which usually have more complex features with a valency greater than four), all this changes dramatically. The Infinity puzzle is also based on the same structure, but this time, it is the rods which are colored instead of the corners.

Figure 5: The 5D symmetry Pegasus and Infinity puzzles and the 6D symmetry Argo and Asterius puzzles.

6. Argo.

The Argo puzzle (named by the ship with Argonauts who were seeking the Golden Fleece), is a puzzle based on the sixth dimensional symmetry of the 6-Simplex (K7). Unlike Chronos, and similar to Pegasus, this higher symmetry, equips the puzzle
with even more complex moves. More specifically, by using the MINEES shape, we now have four choices for IOTs, compared to only one found in Chronos and three in Pegasus. And just like Pegasus, each of those choices provides a different result.

Just like with Chronos and Pegasus (who also belong to the Simplex family) we are able to exchange any two vertices of the MINEES shape while keeping the rest of the puzzle invariant.

7. Hyperion, Happier Cube, and the... Abyss.

Figure 6: The Happier-Cube and the Abyss puzzles based on the Hypercube.

Those are puzzles based on the Hypercube, which has a MAXEES shape, such that the outer cube (made of twelve edges) is of color 1, the inside cube (also twelve edges) is of color 2, and their corners are connected with eight edges of color 3. The goal of those puzzles is to use the only one available IOT (which may be applied in six different directions) to interchange the cube of color 1 with the cube of color 2 (as shown in Figure 3). The Hyperion and Abyss use telescopic rods. The Happier Cube is the same puzzle, using elastic tubes.

8. Colossus (based on the Icositetrachoron, also known as 24-cell)

By using the structure of the Graphidrons, we may construct any graph-related object in any dimension. But no such object (in any dimension) can match the plethora of symmetric properties found in the Colossus puzzle. Being a vertex and edge transitive dual regular polytope just gives a good idea of its exquisite nature. But by adding the rare symmetric property of triality, it unfolds its uniqueness compared to any other structure. No other object of finite symmetry, in any dimension (even higher than 4) could match the symmetric depth of the 24-cell.

The Colossus consists of eight connected octahedrons (each of different color: yellow, purple, blue, red, white, black, brown, and green). There is always one "outside" octahedron and there and an "inside" octahedron. The six corners of the outside octahedron are connected to the six corners of the inside octahedron with the six other octahedrons.

Figure 7: The Colossus puzzle by the Kastellorizo harbour.

The purpose of this puzzle is to interchange the color of the outside octahedron with the color of the inside octahedron. In fact, by manipulating the edges, you may interchange the inside or outside octahedrons with any of the other colored ones. And although this sounds impossible, it is more than possible. The only known person who has managed this feat is well known award winning puzzler Wei Hwa Huang in July 2010 at the IPP30 in Osaka. In Figure 1 the yellow octahedron was the inside octahedron, but in Figure 10, the yellow octahedron is now outside!

9. Afrodite.
The Afrodite puzzle (based on the Rectified Pentachoron) is also known as the "most beautiful puzzle in the universe" because:

1. It has a diamond shape whose external sides correspond to only one color.
2. It can change its (MAXEES shaped) external color to any of five colors.
3. It is covered with a soft flexible fabric, as if it had a skin.

Figure 8: The endoskeleton, and the yellow "skin" state of Afrodite.

Unlike Chronos (where a corner moves through a triangular face) and Hyperion (where a square face moves through a square face), here the IOT involves the movement of an entire "dressed up" tetrahedron through a triangular face. Most of the puzzles described here are based on expandable (telescopic or elastic) rods. Afrodite is the first puzzle ever made with expandable (on a 2:1 ratio) faces. The name of the puzzle also belongs to the most beautiful lady I personally know.

10. Pyramus & Thisbe.

This Tetrahedral Prism puzzle is based on the story of two lovers who lived in the city of Babylon and were never able to meet.

Just like in the story, the blue tetrahedron (Pyramus) can never connect the red tetrahedron (Thisble). But they are always together as their love (represented by the yellow edges that connect the two tetrahedrons) never allows them to be separated. As each of the two lovers search of each other, any of the two tetrahedrons can become external (forcing the other one to become internal.

Figure 9: The "Pyramus and Thisbe" and Cosmos puzzles.

11. Cosmos.

Imagine a cube made of edges and their antipodes are also connected. This is in fact, the complete bipartite graph K4,4.

The goal of this puzzle is swap the positions of the blue and black rods (which form a blue and black square) with the positions of the red and yellow rods (half of which connect the squares and the other half are antipodes). Although it is not related to any polytope (higher than 3D) it has valency equal to four, so it can easily be labelled as a puzzle based on 4D symmetry. It is one of the most difficult puzzles, but for tanglement, not mathematical reasons.

15. Gorgon.

The Petersen Graph is one of the most important structures in Graph Theory, and it would be unimaginable to not have a Graphidron based on it. Besides its artistic beauty by having a pentagon of color 1, connected to a pentagram of color 2, it is also a very interesting puzzle. The goal is to interchange the colors 1 and 2.

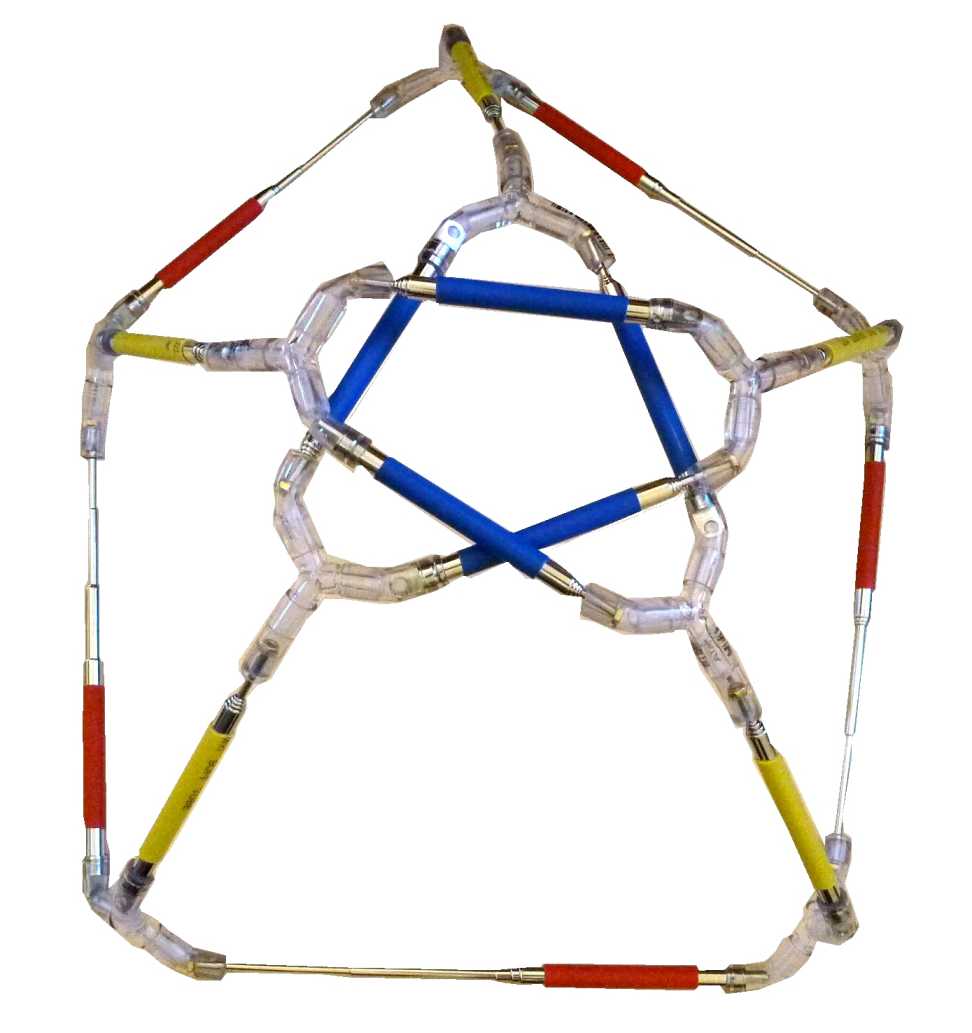
Figure 10: The Gorgon and Cerberus puzzles.

16. Cerberus.
Despite its simplistic appearance, a puzzler will immediately become intimidated by feeling the structure of the Cerberus, based on the based on the Great Triambic Icosahedron Face. The goal of the puzzle is to create a pentagram out of its six rods. And just like the three-headed guard of the Underworld, this puzzle is protecting its secret solution very efficiently.

Graphidron Notation

The notation of the Graphidrons should be more standarised to "loosely" ensure that there are no repetitions of isomorphic cases. Each design is named as G(X,Y,Z), where X = [Types of Faces], Y = [Valency], and Z = [Nr of Vertices]. The variable X refers to the existence of one or more polygon types (by using the number of sides) which exist in the structure. There is no requirement to mention the number of edges as (since we are almost always dealing with regular connected graphs) it is equal to half of Y times Z.

We have the following examples of existing puzzles: Cerberus (based on the Great Triambic Icosahedron Face) G(6,2,6), Heron (based on the Tetrahedron) G(3,3,4), Lernaean Hydra (based on the Triangular Double Helix or Mobius-3 or K3,3) G(4,3,6), Olympus (based on the Square Double Helix or Mobius-4) G(4,3,8), Gorgon (based on the Peterson Graph) G(5,3,10), Chronos (based on the Pentachoron) G(3,4,5), Ananke (colored corners - based on the Pentachoron) G(3,4,5), Hyperion (based on the Hypercube) G(4,4,16), Pyramus and Thisbe (based on the Tetrahedral Prism) G([3,4],4,8), Cosmos (based on the K4,4) G(4,4,8) Pegasus (based on the Hexateron K6). G(3,5,6), Argo (based on the K7) G(3,6,7), Houlis Cube (based on the 16 cell/4-orthoplex) G(3,6,8), Colossus (based on the 24-cell/Icositetrachoron) G(3,8,24).

For more information (photos and videos) regarding all of the above, you may visit "PantazisPuzzles" on facebook.